Binary search algorithm is used to find a number in a sorted list. so, the pre condition for binary search is that the list should be sorted. If the number is found then its index is returned.
This algorithm works on divide and conquer principle.
def binary_search(sortedlist,n,x):
start = 0
end = n - 1
while(start <= end):
mid = (start + end)/2
if (x == sortedlist[mid]):
return mid
elif(x < sortedlist[mid]):
end = mid - 1
else:
start = mid + 1
return -1
n = input("Enter the size of the list: ")
sortedlist = []
for i in range(n):
sortedlist.append(input("Enter %dth element: "%i))
x = input("Enter the number to search: ")
position = binary_search(sortedlist, n, x)
if(position != -1):
print("Entered number %d is present at position: %d"%(x,position))
else:
print("Entered number %d is not present in the list"%x)
Explaination:
we pass the list, the length of the list and the number to search to a function binary_sort
The start and end position is initially 0 and n-1 , where n is the length of the list.
we calculate middle position using mid = (start + end)/2
If the number to be searched is equal to the number at the middle position then it is simply returned
but if its less than the middle number then change end to mid -1 and if its greater than the middle element then start is changed to mid + 1
in the next iteration of the while loop the number is again matched with the new middle element and so on…
you can notice that at each iteration of the loop the search space is reduced to half and thus the number of comparisons is reduced.
the while loop is terminated if start becomes greater or equal to end, that simply means that there is nothing left to search. after the while loop terminates on meeting this condition -1 value is returned to denote that the element was not found.
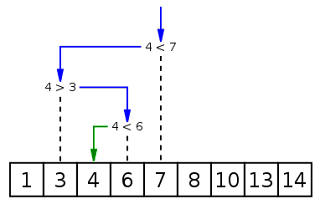
Here is an image from wikipedia, showing Binary Search of a given number 4
Time Complexity:
O(logn)